Python OCC

PythonOCC omogoča enostavnejšo uporabo jedra modelirnika OpenCascade v jeziku Python. Prednost Pythona v primerjavi z C++ je:

• Prenosljivosti. Programi se interpretirajo in jih ni potrebno prevajati zato delujejo na vseh operacijskih sistemih. So pa nekoliko počasnejši.
• Enostavnejša namestitev potrebnih knjižnic, brez zahtevne konfiguracije povezovalnih parametrov, ki so značilni za C++.
• Lažje učenje jezika. V interaktivnem načinu obstaja tudi refleksija oziroma dinamično prepoznavanje možnih ukazov v objektu.

Za vaje je potrebno na Windowsih (tudi 64 bitnih) namestiti naslednje pakete:

1. ​Python 2.6 interpreter jezika z osnovnimi knjižnicami
2. ​wxPython za opravljanje z okni
3. ​PythonOCC povezava Pytona z jedrom OpenCascade

Neobvezno vendar priporočljivo je namesti še:

1. ​iPython za interektivno delo
2. ​NumPy za delo z numeričnimi metodami in matrikami.
3. ​SciPy za delo z znanstvenimi algoritmi.

Pred preizkusom prvih primerov je potrebno nastaviti še pot do interpreterja v Moj računalnik -> Lastnosti -> Dodatne nastavitve sistema -> Spremenljivke okolja ... -> Sistemske spremenljivke -> Path -> Uredi -> Vrednost spremeljivke: in na koncu dodamo ;c:\Python26;. Po tem je potremn računalnik vnovič zagnati.

V primeru, da nam klik na Start->Vsi programi->pythonOCC -> Examples -> Level1 -> HelloWorld -> helloworld.py okno na hitro odpre, vendar modela ne prikaže, imamo težave z OpenGL krmilniki. Najenostavneje težavo odpravimo s spremembo osnovnega prikazovalnika v datoteki C:\Python26\Lib\site-packages\OCC\Display\wxDisplay.py v kateri platformo darwin poistovetimo z win32 tako da del kode v tej datoteki izgleda:

if sys.platform=='win32':
    BaseClass = wx.Panel
else:
    import wx.glcanvas
    BaseClass = wx.glcanvas.GLCanvas

V primeru, da nam namestitveni program nepravilno namesti imenik na C:\OCC ga prestavimo v podimenik C:\Python26\Lib\site-packages

---

Struktura programa v Python OCC

Rabimo uvoziti uporabniški vmesnik, ki nam omogoči preprosto manipulacijo predstavljenega objekta (glava dokumenta):

from OCC.Display.SimpleGui import *

Z ukazno vrstico uvozimo v program knjižnico, ki vsebuje modelno okno ter preprosti uporabniški vmesnik, ki ga lahko uporabimo za prikaz različnih geometrijskih oblik v 3D okolju.

Uvedba funkcij za iniciacijo prikaza:

display, start_display, add_menu, add_function_to_menu = init_display()

Z ukazno vrstico uvedemo v program prikaz v modelnem oknu ter možnost uporabe preprostega menija.

Iniciacija prikaznega okna:

start_display()

S tem ukazom iniciramo modelno okno. Definicija uporabljenih geometrijskih oblik mora biti podana preden se ukaz izvede.

Uporaba miške v uporabniškem vmesniku:

• Rotacija objekta: levi gumb na miški
• Translacija objekta: srednji gumb na miški
• Povečava objekta: desni gumb na miški, premik levo-desno

Uporaba tipkovnice v uporabniškem vmesniku:

• Tipka'w'- prikaz žičnega modela
• Tipka 'e'- prikaz vidnih robov
• Tipka 's'- prikaz volumskega modela
• Tipka 'f'- prikaz celega objekta v prikaznem oknu
• Tipka 'q'- prikaz vidnih robov

Za izdelavo modela v okolju Python OCC je potrebna predhodna uvedba knjižnic OpenCascade (OCC), ki vsebujejo različne nabore ukazov:

from OCC.Display.SimpleGui import *  # Knjižnica z modelnim oknom ter uporabniškim vmesnikom (GUI)
from OCC.gp import *                 # Knjižnica z naborom osnovnih gradnikov -točk
from OCC.GC import *                 # 
from OCC.TopoDS import *             # Knjižnica z naborom topoloških gradnikov (krivulje,...)
from OCC.BRepBuilderAPI import *     # Knjižnica z naborom osnovnih gradnikov skice (vozlišča, robovi, segmenti, mreže ...)
from OCC.BRepPrimAPI import *        # Knjižnica z naborom osnovnih geometrijskih primitivov
from OCC.BRepFilletAPI import *      # Knjižnica z naborom orodij za izdelavo zaokrožitev

V program uvedemo zgolj knjižnice, ki jih tudi rabimo za učinkovito delovanje.

---

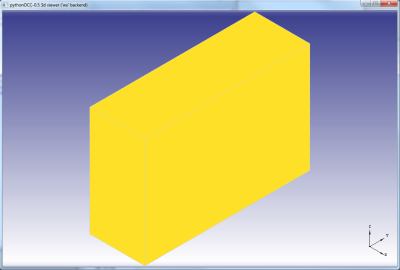
Preprosti program- Primer izdelave izvleka v prostor (Extrude)

Primer izdelave kocke z dimenzijami 10x10x10. Postopek modeliranja v komercialnih modelirnikih (SolidWorks?, Catia, NX, ProEngineer?, Inventor,...) je sledeči:

• izbira ravnine, na katero se nariše skica
  
  
• izris oblike skice (kvadrat)
  
  
• definiranje skice (dimenzije, geometrijske relacije, pozicija v prostoru)
  
  
• izbira ustrezne značilke za izdelavo 3D objekta (Izvlek- Extrude)
  
  
• določitev parametrov izvleka (smer, dolžina izvleka)
  
  
• model je zmodeliran

V okolju Python OCC poteka izris objekta nekoliko drugače. Razložen je preprosti postopek izdelave kocke, ki poteka v večih korakih. Pri izdelavi je potrebno manualno določiti vse parametre, ki jih komercialni modelirnik običajno določi namesto nas.

Korak 01: Izdelava točke v prostoru 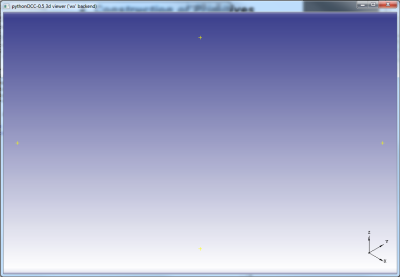Razlaga ukaza za izdelavo točke ​gp__Pnt

Tocka = gp_Pnt(x_1 , y_1 , z_1)

Iz določenih točk lahko naredimo vozlišča. Detajlna razlaga uporabljenega ukaza: ​BRepBuilderAPI__MakeVertex.

Vozlisce = BRepBuilderAPI_MakeVertex(Tocka)

Če hočemo prikazati vozlišča v modelnem oknu, potem je potrebno napisati ukaz za prikaz oblike:

display.DisplayShape(Vozlisce.Shape())

Korak 02: Izdelava robov iz točk

Rob = BRepBuilderAPI_MakeEdge(Zacetna_tocka, Koncna_tocka)

Za izdelavo roba rabimo dva podatka, to je začetna točka ter končna točka robu. Detajlna razlaga uporabljenega ukaza: ​BRepBuilderAPI__MakeEdge. Če hočemo prikazati izdelani rob v modelnem oknu, je potrebno zapisati ukaz:

display.DisplayShape(Rob.Shape())

Korak 03: Izdelava mrežnega modela iz točk

Mreza  = BRepBuilderAPI_MakeWire(Rob1.Edge() , Rob2.Edge() ,Rob3.Edge(), Rob4.Edge())
Mreza2  = BRepBuilderAPI_MakeWire(Mreza.Wire(), Rob1.Edge())

Vsak rob predstavlja svojo geometrijsko obliko v prostoru. Zato moramo, preden naredimo površino te robove združiti v eno samo geometrijo. Pozorni moramo biti, da robovi tvorijo zaprto obliko. Ukaz nam dovoli sočasno uporabo štirih argumentov- robov. Pri tem moramo označiti, da gre za obliko roba [Rob.Edge()]. Kot rezultat dobimo združeno mrežo. Detajlna razlaga uporabljenega ukaza: ​BRepBuilderAPI__MakeWire Če hočemo prikazati izdelani rob v modelnem oknu, je potrebno zapisati ukaz:

display.DisplayShape(Mreza.Shape())

Korak 04: Izdelava površine iz obstoječe mreže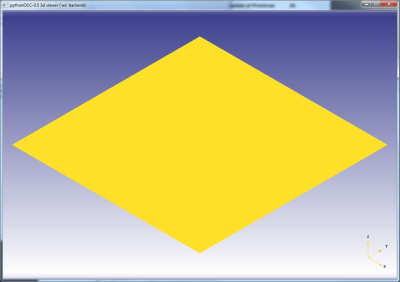

Povrsina = BRepBuilderAPI_MakeFace(Mreza.Wire())

Iz obstoječega zaprtega lika, ki je planaren lahko tvorimo površino. Detajlna razlaga uporabljenega ukaza: ​BRepBuilderAPI__MakeFace Če hočemo prikazati izdelani rob v modelnem oknu, je potrebno zapisati ukaz:

display.DisplayShape(Povrsina.Shape())

Korak 05: Izdelava izvleka v prostor Izdelano površino lahko uporabimo za izdelavo tridimenzionalne oblike. Če hočemo narediti izvlek, je potrebno najprej določiti še parametre vičine izvleka. V ta namen določimo vektor, ki vsebuje podatek o velikosti in smeri izvleka. Razlaga uporabljenega ukaza: ​gp_Vec.

Vektor = gp_Vec(Velikost_X , Velikost_Y, Velikost_Z)

Sledi uporaba ukaza za izdelavo izvleka. Pri tem je potrebno uporabiti podatek o površini ter izdelani vektor. Če hočemo, lahko naredimo tudi neskončno dolgi izvlek v prostor, tako da uporabimo zgolj podatek o izbrani smeri namesto določenega vektorja (uporaba pri Boolovi operaciji odštevanja). Razlaga uporabljenega ukaza: ​BRepFeat__MakePrism.

Izvlek = BRepPrimAPI_MakePrism(Povrsina.Face() , Vektor)
Izvlek = BRepPrimAPI_MakePrism(Povrsina.Face() , Smer)

Barvo modela lhako po želji spremenimo z uporabo ukaza:

display.DisplayColoredShape(Oblika.Shape(), 'BARVA')

Primer programa za izdelavo izvleka:

## Izdelava Izvleka

from OCC.Display.SimpleGui import * 
from OCC.BRepPrimAPI import *
from OCC.gp import *
from OCC.GC import *
from OCC.BRepBuilderAPI import *

display, start_display, add_menu, add_function_to_menu = init_display()

#Izdelava točk v prostoru
T1 = gp_Pnt(0 , 0 , 0)
T2 = gp_Pnt(10 , 0, 0)
T3 = gp_Pnt(10 , 10 , 0)
T4 = gp_Pnt(0, 10 , 0)

#izdelava robov na podlagi definiranih tock
E1 = BRepBuilderAPI_MakeEdge(T1, T2)
E2 = BRepBuilderAPI_MakeEdge(T2, T3)
E3 = BRepBuilderAPI_MakeEdge(T3, T4)
E4 = BRepBuilderAPI_MakeEdge(T4, T1)

#izdelava mreznega modela
Mreza  = BRepBuilderAPI_MakeWire(E1.Edge() , E2.Edge() ,E3.Edge(), E4.Edge())

#Izdelava povrsine
Povrsina = BRepBuilderAPI_MakeFace(Mreza.Wire())

#Izdelava vektorja za izvlek v prostor
Vektor1 = gp_Vec(0 , 0, 10)

#Izdelava priznaticnega telesa- izvlek povrsine v smeri vektorja
Izvlek = BRepPrimAPI_MakePrism(Povrsina.Face() , Vektor1)

#Prikaz izvleka v prikaznem oknu
display.DisplayShape(Izvlek.Shape())

#Sprememba barve modela
display.DisplayColoredShape(Izvlek.Shape(), 'RED')

display.View_Iso() #izometricni prikaz
start_display()

---

Uporaba geometrijskih primitivov

Izdelava kvadra

kvader = BRepPrimAPI_MakeBox(dolzina_X, dolzina_Y, dolzina_Z)
kvader = BRepPrimAPI_MakeBox(Tocka1, dolzina_X, dolzina_Y, dolzina_Z)
kvader = BRepPrimAPI_MakeBox(Tocka1, Tocka2)

Z ukazom ​BRepPrimAPI__MakeBox izdelamo tridimenzionalni model oblike kvadra. Pri tem lahko uporabimo več različnih argumentov:

• (dolzina_X, dolzina_Y, dolzina_Z) ... kvader določimo z razdaljami posameznih robov
  
  
• (Tocka1, dolzina_X, dolzina_Y, dolzina_Z) ... kvader se prične izrisovati od točke 1 (X,Y,Z) dalje inje določen z razdaljami posameznih robov
  
  
• (Tocka 1, Tocka2) ... kvader določimo s koordinatami dveh točk, ki ježita v nasproti ležečih ogliščih

Izdelava izvleka pod kotom nagiba

kvader= BRepPrimAPI_MakeWedge(dolzina_X, dolzina_Y, dolzina_Z, dolzina_X2)
kvader= BRepPrimAPI_MakeWedge(dolzina_X, dolzina_Y, dolzina_Z, dolzina_Xmin, dolzina_Zmin, dolzina_Xmax, dolzina_Zmax)
kvader= BRepPrimAPI_MakeWedge(dolzina_X, dolzina_Y, dolzina_Z, dolzina_X/2, 0, dolzina_X/2, dolzina_Z)
kvader= BRepPrimAPI_MakeWedge(dolzina_X, dolzina_Y, dolzina_Z, dolzina_X/2, dolzina_Z/2, dolzina_X/2, dolzina_Z/2)

Z ukazom ​BRepPrimAPI__MakeWedge izdelamo tridimenzionalni model oblike kvadra s koti nagiba. Pri tem lahko uporabimo več različnih argumentov:

• (dolzina_X, dolzina_Y, dolzina_Z, dolzina_X2) ... določimo razdalje posameznih robov kvadra, ter dimenzijo spremenjenega roba X
  
  
• (dolzina_X, dolzina_Y, dolzina_Z, dolzina_Xmin, dolzina_Zmin, dolzina_Xmax, dolzina_Zmax) ... določimo razdalje posameznih robov kvadra, ter minimalne in maksimalne dimenzije robov X in Z
• (dolzina_X, dolzina_Y, dolzina_Z, dolzina_X/2, 0, dolzina_X/2, dolzina_Z) ... določimo razdalje posameznih robov kvadra, ter dimenzijo spremenjenega roba Z
  
  
• (dolzina_X, dolzina_Y, dolzina_Z, dolzina_X/2, dolzina_Z/2, dolzina_X/2, dolzina_Z/2)... določimo razdalje posameznih robov kvadra, preostali argumenti nam podajo obliko piramide

Izdelava valja

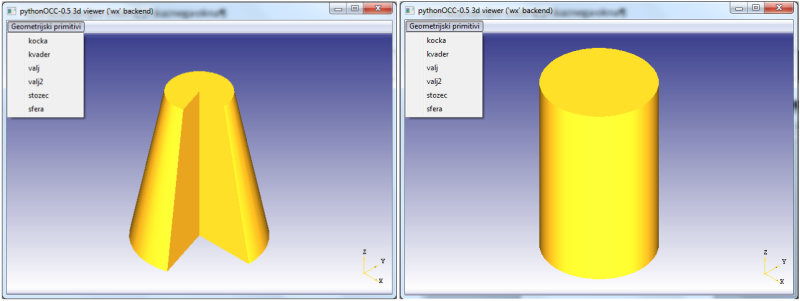
valj= BRepPrimAPI_MakeCylinder(Radij, Visina, Kot_radiani)
valj= BRepPrimAPI_MakeCylinder(Os, Radij, Visina, Kot_radiani)

Z ukazom ​BRepPrimAPI__MakeCylinder izdelamo tridimenzionalni model oblike valja. Pri tem lahko uporabimo več različnih argumentov:

• (Radij, Visina) ... izdelamo valj z določenim radijem in višino
• (Radij, Visina, Kot_radiani) ... izdelamo delj valja za nastavljen kot z določenim radijem in višino
• (Os, Radij, Visina, Kot_radiani) ... izdelamo delj valja za nastavljen kot z določenim radijem in višino in ki ima nastavljeno poljubno os

Os valja definiramo kot:

Tocka = gp_Pnt(X, Y, Z)         #definicija tocke
normala = gp_DX()               #smer normale
os = gp_Ax2(Tocka, normala)     #definicija osi

Izdelava stožca

stozec= BRepPrimAPI_MakeCone(Radij_1, Radij_2, Visina, Kot_radiani)
stozec= BRepPrimAPI_MakeCone(Os, Radij_1, Radij_2, Visina, Kot_radiani)

Z ukazom ​BRepPrimAPI__MakeCone izdelamo tridimenzionalni model oblike stožca. Pri tem lahko uporabimo več različnih argumentov:

• (Radij_1, Radij_2, Visina) ... izdelamo stožec z osnovo radija 1 ter na višini H z radijem 2
  
  
• (Radij_1, Radij_2, Visina, Kot_radiani) ... izdelamo delni stožec, določen s kotom, z osnovo radija 1 ter na višini H z radijem 2
  
  
• (Os, Radij_1, Radij_2, Visina, Kot_radiani) ... izdelamo delni stožec okoli izbrane osi, določen s kotom, z osnovo radija 1 ter na višini H z radijem 2

Izdelava sfere

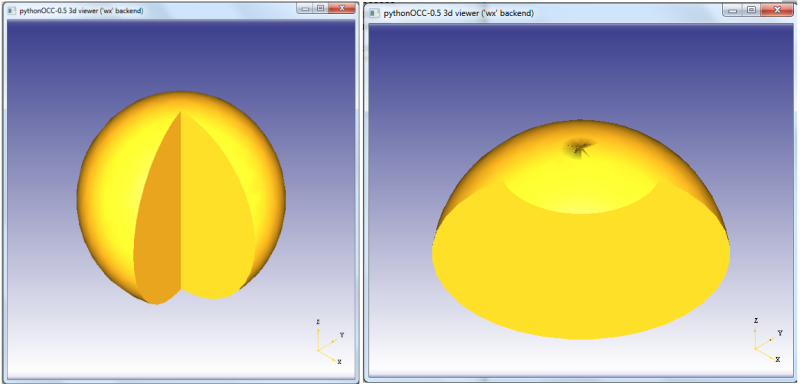
sphere= BRepPrimAPI_MakeSphere(Radij, Kot_radiani)
sphere= BRepPrimAPI_MakeSphere(Radij, Kot_a1_rad, Kot_a2_rad)
sphere= BRepPrimAPI_MakeSphere(Radij, Kot_a1_rad, Kot_a2_rad, Kot_radiani)

Z ukazom ​BRepPrimAPI__MakeSphere izdelamo tridimenzionalni model oblike sfere. Pri tem lahko uporabimo več različnih argumentov:

• (Radij) ... izdelave sfere z radijem
• (Radij, Kot_radiani) ... izdelave delne sfere z radijem
• (Radij, Kot_a1_rad, Kot_a2_rad) ... izdelave sfere, ki ima odstanjen sredinski del pod kotom 1 in kotom 2
  
  
• (Radij, Kot_a1_rad, Kot_a2_rad, Kot_radiani) ... izdelave delne sfere, ki ima odstanjen sredinski del pod kotom 1 in kotom 2

Izdelava torusa

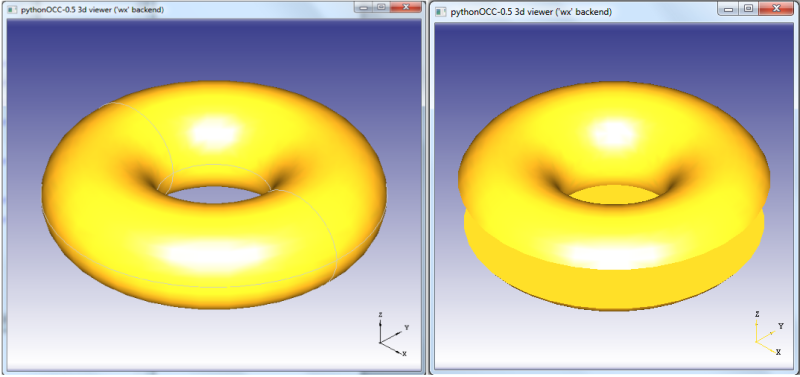
torus= BRepPrimAPI_MakeTorus(Radij_torusa, Radij_prereza)
torus= BRepPrimAPI_MakeTorus(Radij_torusa, Radij_prereza, Kot_radiani)
torus= BRepPrimAPI_MakeTorus(Radij_torusa, Radij_prereza, Kot_a1_rad, Kot_a2_rad)

Z ukazom ​BRepPrimAPI__MakeTorus izdelamo tridimenzionalni model oblike torusa. Pri tem lahko uporabimo več različnih argumentov:

• (Radij_torusa, Radij_prereza) ... izdelava torusa s središčnim radijem ter polmerom prereza
  
  
• (Radij_torusa, Radij_prereza, Kot_radiani) ... izdelava delnega torusa s središčnim radijem ter polmerom prereza
  
  
• (Radij_torusa, Radij_prereza, Kot_a1_rad, Kot_a2_rad) ... izdelava delnega torusa, ki ima odstanjen sredinski del pod kotom 1 in kotom 2

Izdelava izvleka

Izvlek = BRepPrimAPI_MakePrism(Povrsina , Vektor)
Izvlek = BRepPrimAPI_MakePrism(Povrsina , Smer)

Z ukazom ​BRepPrimAPI__MakePrism izdelamo tridimenzionalni prizmatični model. Pri tem lahko uporabimo več različnih argumentov:

• (Povrsina , Vektor) ... izberemo obstoječo površino ter jo izvlečemo za velikost vektorja
• (Povrsina , Smer) ... izberemo obstoječo površino ter jo izvlečemo v željeni smeri

Izdelava krožnega izvleka

Vrtenina = BRepPrimAPI_MakeRevol(Povrsina , Os)
Vrtenina = BRepPrimAPI_MakeRevol(Povrsina , Os, Kot_radiani)

Z ukazom ​BRepPrimAPI__MakeRevol izdelamo tridimenzionalni osnosimetričnimodel. Pri tem lahko uporabimo več različnih argumentov:

• (Povrsina , Os) ... zavrtimo izbrano površino okoli osi
• (Povrsina , Os, Kot_radiani) ... zavrtimo izbrano površino za kot okoli osi

---

Uporaba menijev znotraj prikaznega okna

Najprej je potrebno definirati funkcije, ki izvršijo ukaz (izdelajo neko obliko). Pri tem pred izrisom oblike počistimo modelno okno obstoječih oblik z ukazom [display.EraseAll?()].

def Funkcija(event=None):
    display.EraseAll()
    #definicija prikazane oblike
    display.DisplayShape(Oblika.Shape())

Izdelava menija

add_menu('Ime_menija')
add_function_to_menu('Ime_menija',Funkcija1)
add_function_to_menu('Ime_menija',Funkcija2)

Boolova algebra

Poznamo tri operacije Boolove algebre: Seštevanje, Odštevanje ter Presek. Za uporabo imamo na voljo knjižnico ukazov BRepAlgoAPI.

from OCC.BRepAlgoAPI import *

Seštevanje (Fusion) 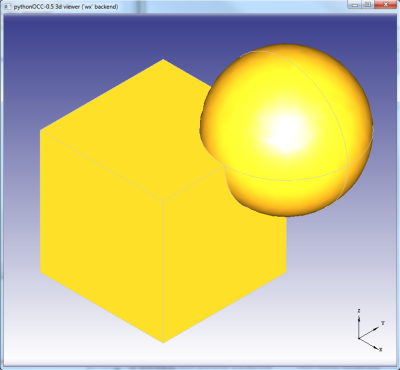Operacija seštevanja objektov se izvaja z uporabo ukaza ​BRepAlgoAPI__Fuse, kjer dodamo kot argumente 3D obliki, ki ju želimo združiti:

sestevanje = BRepAlgoAPI_Fuse(Oblika1,Oblika2)

Presek (Common) Operacija izdelave preseka objektov se izvaja z uporabo ukaza ​BRepAlgoAPI__Common, kjer dodamo kot argumente 3D obliki, med katerimi želimo poiskati skupni volumen:

presek = BRepAlgoAPI_Common(Oblika1,Oblika2)

Odštevanje (Cut) Operacija odštevanjaobjektov se izvaja z uporabo ukaza ​BRepAlgoAPI__Cut, kjer dodamo kot argumente 3D obliki. Prvi argument predstavlja osnovno obliko, drugi argument pa predstavlja geometrijo, ki jo odštevamo. Vrstni red je v tem primeru pomemben!

odstevanje = BRepAlgoAPI_Cut(Objekt1, Objekt2)

Geometrijske transformacije

Translacija objekta (Transform) Za premik objekta v prostoru se uporabi funkcija za translacijo. Pri tem je potrebno najprej določiti vektor premika, nato pa izberemo obliko, ki jo želimo premakniti v prostoru. Preprosta koda je zapisana:

Premik = gp_Vec(U_X, U_Y, U_Z)
Translacija = gp_Trsf()
Translacija.SetTranslation(Premik)
rezultat = BRepBuilderAPI_Transform(Oblika, Translacija).Shape()

Rotacija objekta (Rotation) 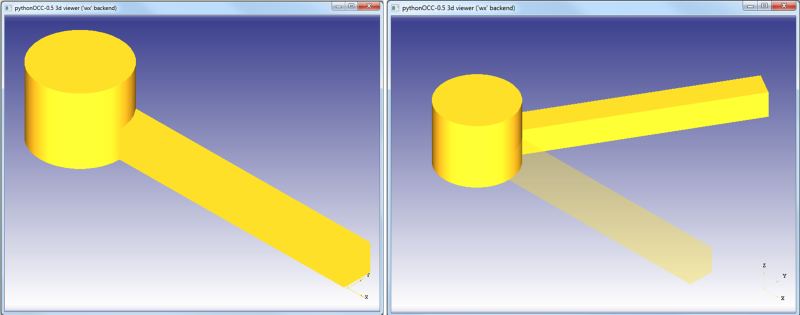V kolikor želimo obstoječi objekt rotirati, je potrebno določiti najprej referenčno točko, ki služi kot lokacija osi vrtenja, ter nato določiti še rotacijsko os s smerjo vektorja. Potrebno je tudi določiti kot rotacije, ki ga določimo v radianih. Nazadnje izberemeo obliko, ki jo hočemo zavrteti okoli izbrane osi. Preprosti algoritem je zapisan:

LokacijaOsi = gp_Pnt(U_X, U_Y, U_Z)
RotacijaOs = gp_Ax1(LokacijaOsi, gp_Dir(Smer_X,Smer_Y,Smer_Z))
TransfRot = gp_Trsf()
TransfRot.SetRotation(RotacijaOs, Kot_radiani)
rezultat = BRepBuilderAPI_Transform(Oblika, TransfRot).Shape()

Aplicirane značilke