NonCoincidentDEC enables non-conservative remapping of fields between two parallel codes. The computation is possible for 3D meshes and 2D meshes. It is not available for 3D surfaces.
The computation enables fast parallel localization, and is based on a point in element search, followed by a field evaluation at the point location. Thus, it is typically faster than the InterpKernelDEC which uses a conservative remapping (i.e. the same algorithms of volume intersection as in the sequential remapper) It is particularly true for the initialisation phase (synchronize() method) which has a significant computation cost in InterpKernelDEC-det.
In the present version, only fields lying on elements ("P0") are considered. The value is estimated by locating the barycenter of the target side cell in a source cell and sending the value of this source cell as the value of the target cell.
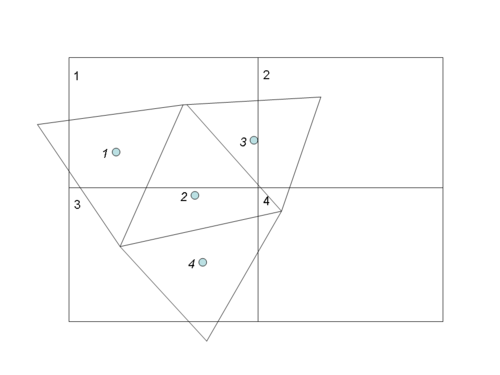
Example showing the transfer from a field based on a quadrangular mesh to a triangular mesh. The triangle barycenters are computed and located in the quadrangles. In a P0-P0 interpolation, the value on the quadrangle is then applied to the triangles whose barycenter lies within.
A typical use of
NonCoincidentDEC encompasses two distinct phases :
- A setup phase during which the intersection volumes are computed and the communication structures are setup. This corresponds to calling the NonCoincidentDEC::synchronize() method.
- A use phase during which the remappings are actually performed. This corresponds to the calls to sendData() and recvData() which actually trigger the data exchange. The data exchange are synchronous in the current version of the library so that recvData() and sendData() calls must be synchronized on code A and code B processor groups.
The following code excerpt illutrates a typical use of the NonCoincidentDEC class.
...
NonCoincidentDEC dec(groupA, groupB);
dec.attachLocalField(field);
dec.synchronize();
if (groupA.containsMyRank())
dec.recvData();
else if (groupB.containsMyRank())
dec.sendData();
...
Computing the field on the receiving side can be expressed in terms of a matrix-vector product : 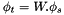 , with
, with 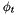 the field on the target side and
the field on the target side and  the field on the source side. In the P0-P0 case, this matrix is a plain rectangular matrix with one non-zero element per row (with value 1). For instance, in the above figure, the matrix is :
the field on the source side. In the P0-P0 case, this matrix is a plain rectangular matrix with one non-zero element per row (with value 1). For instance, in the above figure, the matrix is :
![\[ \begin{tabular}{|cccc|} 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ \end{tabular} \]](form_84.png)
 Public Member Functions inherited from MEDCoupling::DEC
Public Member Functions inherited from MEDCoupling::DEC Public Member Functions inherited from MEDCoupling::DECOptions
Public Member Functions inherited from MEDCoupling::DECOptions Protected Attributes inherited from MEDCoupling::DEC
Protected Attributes inherited from MEDCoupling::DEC
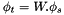 , with
, with 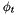 the field on the target side and
the field on the target side and 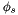 the field on the source side. In the P0-P0 case, this matrix is a plain rectangular matrix with one non-zero element per row (with value 1). For instance, in the above figure, the matrix is :
the field on the source side. In the P0-P0 case, this matrix is a plain rectangular matrix with one non-zero element per row (with value 1). For instance, in the above figure, the matrix is : ![\[ \begin{tabular}{|cccc|} 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ \end{tabular} \]](form_84.png)